Mergesort

Introduction

Merge sort is a popular sorting algorithm that uses the divide and conquer strategy.

• How it works
  • Algorithm
  • Analysis for special case

How it works

The mergesort algorithm recursively divides an array into two halves. Then the algorithm will sort each half and merge it with it's other half. Here is an example below.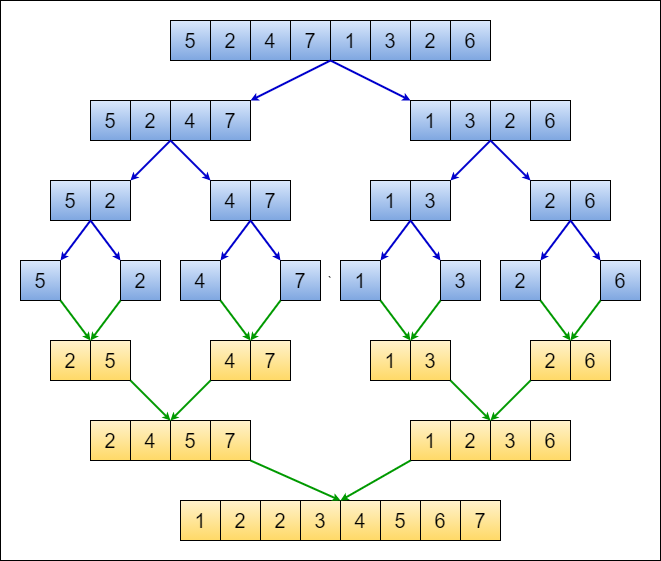

We will now only focus on the merging part of the algorithm. We will focus on the last operation, merging the sorted halves, $A$ and $B$ of the entire array into $C$.

We first compare the smallest(first) element of $A$, with the smallest (first) element of $B$. The smallest of the two becomes the first element in the sorted result, $C$.

We now increment the list which consisted the smallest number. And the merge process is continued the same way.

The merge process is continued until one of the sequences has no more elements in it. The sequences might also contain the same number of elements as in this case.

Let $M(m,n)$ be the worst-case number of key comparisons to merge two sorted sequences of length $m$ and $n$. Then,

The reasoning is simple. After each comparison, one element will be popped out until only one element remains.

However, for the special case of when the two sorted sequences are of equal length, the worst-case number of comparisons becomes,

What is the best-case number of key-comparisons? It is $min(m,n)$. That is, all the elements of the shortest sequence are smaller than all elements of the longer sequence.

Algorithm

def merge_sort(array:list):
    if len(array) > 1:

        #find the mid point
        mid:int = len(array)//2

        #separe to a left block and right block
        L:list[int] = array[:mid]
        R:list[int] = array[mid:]

        ##sort the first hald
        merge_sort(L)

        ##sort the second half
        merge_sort(R)

        i=j=k=0

        ##copy L,R sor sorted array
        while i < len(L) and j < len(R):
            if L[i] <= R[j]:
                array[k] = L[i]
                i+=1
            else:
                array[k] = R[j]
                j+=1
            k+=1


        while i < len(L):
            array[k] = L[i]
            i+=1
            k+=1

        while j < len(R):
            array[k] = R[j]
            j+=1
            k+=1

array = [1,-2,3,90,86,89]
merge_sort(array=array)
print(array)

Analysis for special case

when $n=2^k$

Let $T(n)$ be the worst-case time to sort $n$ elements (by recursive Mergesort). The worst-case time to recursively sort each half is $T(\frac {n}{2})$. And the time to merge the two sorted halves is $O(n)$, which means $\le cn$ for some constant $c$. Therefore,

Solving by substitution we get

Therefore,