Binary Trees Intro

• Definitions and Terminologies
• Implementation
• Running script

Introduction

In computer science, a binary tree is a data structure than consists of a root node which can have a left child and a right child. The common approach is for the left child to be $<$ then its parent node while the right child is greater than its parent node. Below is an example of a binary tree.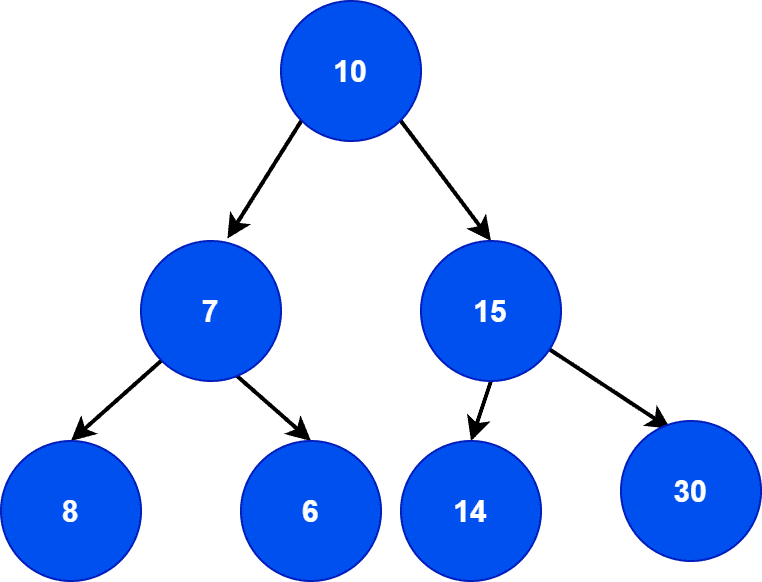

Definitions and Terminologies

Depth or Level Number

• The depth of a node will be it's distance from the root, starting with the root at level 0.

Height of node

• Height of node will be it's distance to the furthest leaf under it, where a leaf (node with no children) node has height 0.
• Let h denote the height of the tree.

Full Binary Tree

• A full-binary tree of height h is a binary tree where all nodes at levels $0,1,...,h-1$ have exactly two children, and all leaves are at level $h$. The Example above is a full-binary tree.

• It's also very easy to see that the left-child of node $i$ will be $2i$ and its right child will be $2i+1$ given that the root node is numbered 1.

• The number of nodes in a full-binary tree is

  $$n = 1+2+4+...+2^h = 2^{h+1}-1$$

• Therefore, the height $h$ in a full-binary tree as a function of $n$ is:

  $$h = \log_2(n+1)-1 = \lfloor \log_2n \rfloor$$

Complete Binary Tree

• A complete-binary-tree allows for an arbitrary number of nodes n by trimming the nodes of a full-binary-tree at the bottom-level, starting with the rightmost node at the bottom level, and removing as many nodes as needed.
• This is a great article for more info and visuals.

Implementation

class Node:
    def __init__(self, value:int):
        self.value = value
        self.left = None
        self.right = None

class BST:
    def __init__(self):
        self.root = None
    def insert(self, value:int):
        node = Node(value)
        if self.root == None:
            self.root = node
            return
        curr = self.root
        while(True):
            if node.value >= curr.value:
                if curr.right == None:
                    curr.right = node
                    return

                curr = curr.right
            else:
                if curr.left == None:
                    curr.left = node
                    return
                curr = curr.left
    def inorder(self, root):
        if root:
            self.inorder(root.left)
            print(root.value, end=' ')
            self.inorder(root.right)

Running script

if __name__ == "__main__":
    import random
    bst = BST()

    for i in range(10):
        bst.insert(random.randint(1,100))
    bst.inorder(bst.root)
    print("")